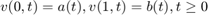HW 1.2.1
Contents
Initial-boundary-value Problem
where 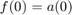 , and
, and 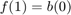
Numerical Solution
Using 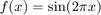 ,
, 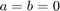 , and
, and 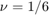
f_ = @(x)(sin(2 * pi * x)); a = 0; b = 0; nu = 1 / 6;
In domain ![$[0, 1] \times [0, 1]$](hw_1_2_1_eq12464155907289493271.png) , let
, let 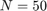 ,
, 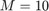 , a.k.a
, a.k.a 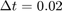 ,
, 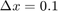
dx = 0.1; dt = 0.02; T = round(1 / dt); X = round(1 / dx); x = 1; t = 1; M = x * X; N = t * T;
Let 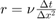
r = nu * dt / dx / dx;
Setting domain and boundary value
x_ = 0 : dx : 1; t_ = 0 : dt : t; [X_, T_] = meshgrid(x_, t_); f = f_(x_); u = zeros(size(X_)); u(1, :) = f;
It is acknowledged that using central difference method to solve this eqution, which indicating the solution like
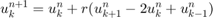
where notation 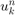 indicating the numerical solution of
indicating the numerical solution of  at the point
at the point 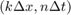
for jj = 1 : N for kk = 2 : M u(jj + 1, kk) = (1 - 2 * r) * u(jj, kk) ... + r * (u(jj, kk - 1) + u(jj, kk + 1)); end end figure; mesh(X_, T_, u); xlabel('x'); ylabel('t'); zlabel('u(numerical)');
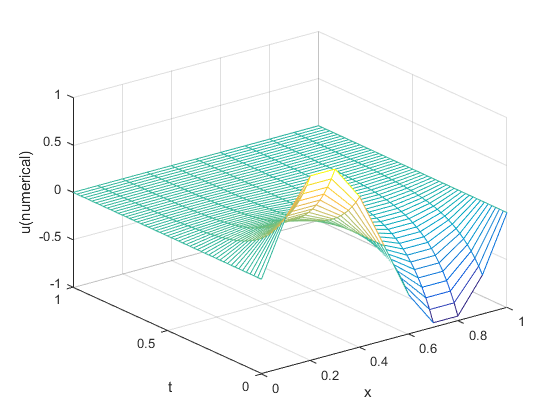
Analytical Solution
Notice that the analytical solutions following the form like
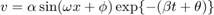
By using the method of undetermined coefficients, the solution is as follows
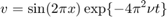
u_exact = sin(2 * pi * X_) .* exp( (-4 * pi * pi * nu) * T_); figure; mesh(X_, T_, u_exact); xlabel('x'); ylabel('t'); zlabel('u(exact)');
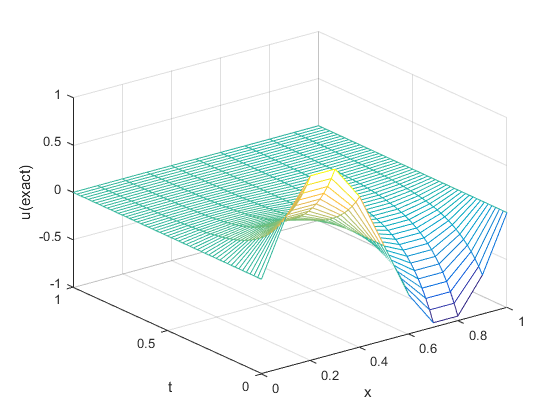
Error
delta = u_exact - u; err = max(abs(delta(:))); figure; mesh(X_, T_, u_exact - u); xlabel('x'); ylabel('t'); zlabel('\Deltau'); fprintf('max error = %f\n', err);
max error = 0.011980
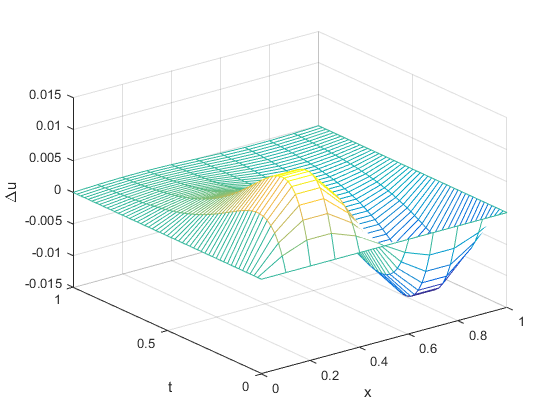
Value of Slices
function plotSlice( t_slice, dt, u, u_exact, x_ ) t_slice_id = round(t_slice / dt) + 1; u_slice_num = u(t_slice_id, :); u_slice_num = u_slice_num(:); u_slice_ext = u_exact(t_slice_id, :); u_slice_ext = u_slice_ext(:); figure; hold on; plot(x_, u_slice_num, 'r-', x_, u_slice_ext, 'g-'); legend('numerical', 'analytical'); xlabel('x'); ylabel('u'); u_slice_err = max(abs(u_slice_num - u_slice_ext)); fprintf('when t = %.2f, max error = %f\n', t_slice, u_slice_err); end
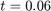
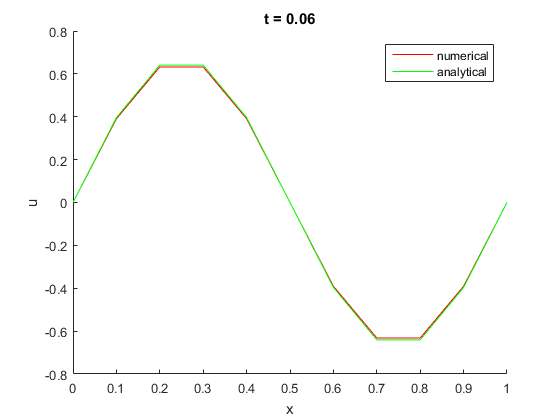
plotSlice( 0.06, dt, u, u_exact, x_ );
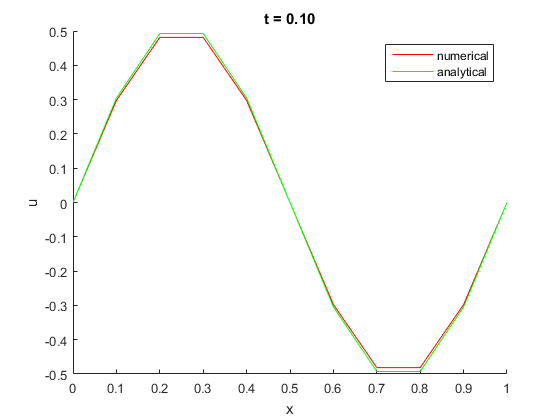
plotSlice( 0.1, dt, u, u_exact, x_ );
plotSlice( 0.9, dt, u, u_exact, x_ );
when t = 0.06, max error = 0.008771 when t = 0.10, max error = 0.011185 when t = 0.90, max error = 0.000476
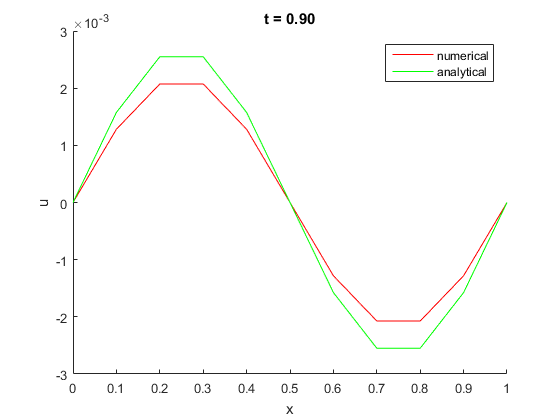
Slice of 
It's known that the formulation is stable if and only if 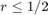 , which indicating
, which indicating  is defined under the constraint that
is defined under the constraint that 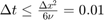 .
.
t = 50; dt = 0.01; N = round(t / dt); t_ = 0 : dt : t; r = nu * dt / dx / dx; [X_, T_] = meshgrid(x_, t_); u_1 = f; u_2 = f; u_2(1) = 0; u_2(M + 1) = 0; for jj = 1 : N for kk = 2 : M u_1(kk) = (1 - 2 * r) * u_2(kk) + r * (u_2(kk - 1) + u_2(kk + 1)); end u_2 = u_1; end u_exact_2 = sin(2 * pi * x_) .* exp( (-4 * pi * pi * nu) * 50); u_slice_err = max(abs(u_1 - u_exact_2)); fprintf('when t = %.2f, max error = %f\n', 50, u_slice_err);
when t = 50.00, max error = 0.000000
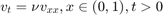
![$v(x, 0) = f(x), x \in [0, 1]$](hw_1_2_1_eq17281590763160515965.png)